前言

機器學習經過訓練(Trainning)、評估(Evaluation)後，就可以得到準確率(Accuracy)、精確率(Precision)、召回率(Recall)、F1 Score、『ROC/AUC 曲線』等各項效能指標[1][2]，如果準確率等於99%，我們真的就可以放心使用了嗎? 如果有兩個模型各有100筆及10萬筆訓練資料，且準確率都等於99%，那它們是一樣可靠嗎? 以下我們就來好好的探討這個問題。

假設檢定(Hypothesis Testing)

直覺上，我們知道愈多樣本資料，可信度越高，但是，應該怎樣以學理說明呢? 另一個問題，如果要做一個可信賴的模型需要多少樣本資料呢? 要回答這個問題前，先要了解『假設檢定』(Hypothesis Testing)、檢定力分析(Power Analysis)。

假設檢定通常是要檢驗某項實驗是否有顯著性的效果，例如，要檢驗新藥是否有效，我們會將病人分為兩組，一組為『控制組』(Control Group)，只服用安慰劑，另一為『干預組』(Intervention Group)，則服用新藥，經過一段時間觀察，就這些樣本判斷新藥是否有『顯著性』的效果，而非『隨機性的抽樣誤差』造成的。一般會以較嚴謹的態度來作判斷，採用1.96倍(95%)、2倍(95.45%)或3倍(99.73%)標準差作為判定基準，只有超出此一範圍，我們才可以大膽假設，新藥應該是有效，並非是湊巧。

一般會使用t統計量來檢驗平均數(Mean)是否有差異，公式如下：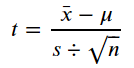

實驗會分成兩種結果：

• 虛無假設(Null Hypothesis, H0)：μ1 = μ2 或是 μ1 - μ2 = 0
• 對立假設(Alternative Hypothesis, H1)：μ1 > μ2 或是 μ1 - μ2 > 0

以所有樣本計算p值，假如落在1.96倍(95%)、2倍(95.45%)或3倍(99.73%)標準差之外，就判定H1假設成立，新藥有效。通常我們會定義α值作為檢驗的標準，例如5%，即落在1.96倍標準差(95%)之外，就是效果顯著，而實驗的結果就是依照t統計量公式計算CDF(Cumulative Distribution Function，累積分配函數)，換算為p值(1-CDF)，它如果小於α值，也就是說實驗結果落在設定的1.96倍標準差的右邊，那就判定H1假設成立，反之，就是『不能拒絕』H0假設(心不甘情不願?)。

實作

了解假設檢定的定義後，我們就隨機產生『控制組』(Control Group)、『干預組』(Intervention Group) 兩組樣本，進一步判斷新藥是否有『顯著性』的效果。計算很簡單，scipy套件直接支援t檢定的函數(ttest_rel)，它預設是雙尾(two-tailed)假定，對立假設為 μ1 > μ2 或 μ1 < μ2 ，以新藥為例，應該只作右尾(right-tailed)檢定，只關注 μ1 > μ2，因此，算出來的p值要減半，如下圖：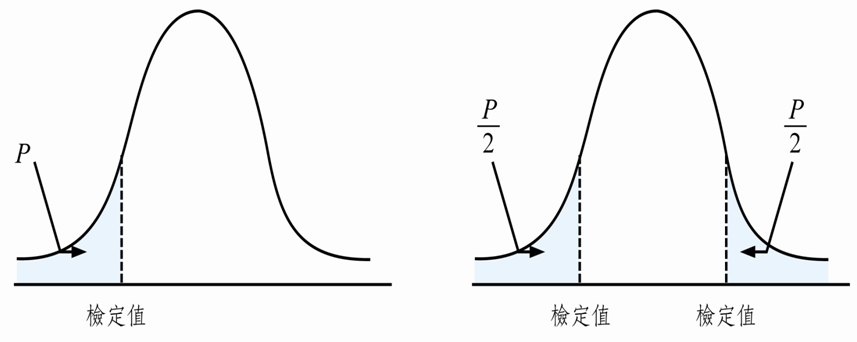

計算過程如下程式所示：

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 隨機產生『控制組』(Control Group)、『干預組』(Intervention Group) 樣本
np.random.seed(123)
control_group = np.random.normal(59.45, 1.5, 100)
intervention_group = np.random.normal(60.05, 1.5, 100)

# ttest_rel 預設為雙尾假定
t,p = stats.ttest_rel(intervention_group, control_group)
# p值要減半，變成單尾假定
p1 = '%f' % (p/2)
print("t-statistic:" + str(t))
print("p-value:" + str(p1))

# 繪圖
pop = np.random.normal(control_group.mean(), control_group.std(), 100000)
# calculate a 90% confidence interval. 10% of the probability is outside this, 5% in each tail
ci = stats.norm.interval(0.90, control_group.mean(), control_group.std())
plt.hist(pop, bins=100)
# show the hypothesized population mean
plt.axvline(pop.mean(), color='yellow', linestyle='dashed', linewidth=2)
# show the right-tail confidence interval threshold - 5% of propbability is under the curve to the right of this.
plt.axvline(ci[1], color='red', linestyle='dashed', linewidth=2)
# show the t-statistic - the p-value is the area under the curve to the right of this
plt.axvline(pop.mean() + t*pop.std(), color='magenta', linestyle='dashed', linewidth=2)
plt.show()

結果如下，紅色為α值，本例為5%，即1.96倍(95%)標準差所在位置，而綠色為p值所在位置，或者比較t值(2.34>1.96)，推斷H1成立。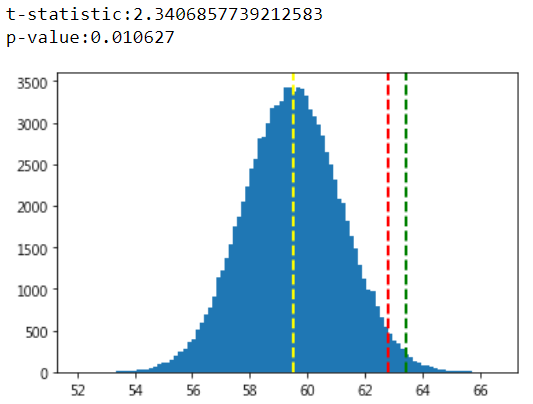

結論

以上假設檢定說明，省略很多細節，因為筆者只想說明效能衡量指標與假設檢定的關聯，結論是，如果要證明一個模型真正具有辨識或預測能力，除了準確率(Accuracy)、精確率(Precision)、召回率(Recall)、F1 Score、『ROC/AUC 曲線』等各項效能指標外，若能額外進行假設檢定，應該會更具說服力。

但是，假設檢定也有一個致命的缺陷，就是所謂的P-Hacking，如果，有人實驗很多次，但他刻意只挑有『顯著性差異』的實驗來發表，外人很難從檢定結果看出此一問題，除非他人也重複實驗一次，否則，很難辨其真偽。

另一個問題，如果要作一個可信賴的模型，我們需要蒐集多少樣本資料呢? 檢定力分析(Power Analysis) 可以解答這個問題，筆者再努力K書，下次再談了。

由於筆者離開學校多年，有關理論的部分，要解釋清楚，實在超出個人能力，文內如有疏漏或謬誤，就請大家指正了。